17年4月底回到学校准备毕业论文,6月答辩,年轻真的杠,一周写一篇毕业设计,就为了一篇1200块卖给同学的钱,现在老了,没那么拼了,那时候卖亏了,看淘宝都是3000块一篇的
0x00 缩略语和关键术语定义
信息隐藏
信息隐藏是把机密信息隐藏在大量信息中不让对手发觉的一种方法。信息隐藏的方法主要有隐写术、数字水印技术、可视密码、潜信道、隐匿协议等。本文主要是改进在数字图像中使用隐写术的算法,改进了LSB算法和亚仿射变化结合的信息隐藏算法
LSB算法
LSB(LeastSignificant Bits)算法:将秘密信息嵌入到载体图像像素值(单位:Byte)的最低有效位,也称最不显著位,改变这一位置对载体图像的品质影响最小
LSB算法基本步骤:
- 将原始载体图像的空域像素值转换成二进制比特序列
- 用二进制秘密信息中的每一比特信息替换与之相对应的载体数据的最低有效位
- 将得到的含秘密信息的二进制数据转换像素值,从而获得含秘密信息的图像
亚放射变换

这是一种几何变化的性质,给定N阶数字图像会在多次进行上面的变化后,每个像素点会被置乱均匀分布在图像中,次数达到一定周期以后,会复原成原图像
原图

经过亚放射变换置乱30次的样子

复原之后的样子

基于这种性质,可以将亚仿射变化用于图像置乱,并利用矩阵编码思想改进LSB的嵌入方式,使隐藏的信息均匀分布到图像中,而不像传统LSB算法使信息集中再某个部分,从而使嵌入数据获得了较好的抗隐写分析能力
隐写分析
隐写分析(steganalysis)是指在已知或未知嵌入算法的情况下,从观察到的数据检测判断其中是否存在秘密信息,分析数据量的大小和数据嵌入的位置,并最终破解嵌入内容的过程。也就是对抗信息隐藏技术的隐写术的一种方式。本文中用来分析改进后算法的效果。
目前一些针常用的LSB信息隐藏分析方式:
- 直方相交距离公式,计算直方相交距离公式的值,越接近1表示隐藏的信息越不容易被发现
- 余弦函数公式,计算余弦函数公式的值,越接近1表示隐藏的信息越不容易被发现
- RS方法(regular and singular groups method)能以很高的精度估计出图像中信息隐藏的比率,结果越小越好
- 频度直方图,直观图像显示,和原图比对视觉差距越小越好
0x01 原有方案的缺点
现有的技术方案
《袁占亭,张秋余,刘洪国,彭铎. 一种改进的LSB数字图像隐藏算法[J]. 计算机应用研究,2009,(01):372-374+377.》这篇论文提出了这种基于亚仿射变化的信息隐藏算法,主要步骤是:
- 将图片用亚仿射变化进行适当次数的置乱
- 需要隐藏的信息用LSB算法嵌入置乱后的图像
- 根据亚仿射变换的周期将图片继续进行亚仿射变化,直到达到亚仿射变化的周期变回原来的图片
- 这种方案通过亚仿射变化用于图像置乱,并利用矩阵编码思想改进LSB的嵌入方式,使隐藏的信息均匀分布到图像中,而不像传统LSB算法使信息集中再某个部分,从而使嵌入数据获得了较好的抗隐写分析能力
现有技术的缺点
上面现有技术方案中提到的算法的亚仿射变化在不同图像尺寸所需周期如下表(原论文中提供):
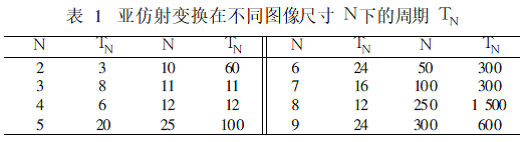
我们可以发现图像在100*100像素的周期就高达数百次,根据上表,基本可以得出图像越大周期越大的趋势,当前常用图片满足主流屏幕1080p的1920*1080,所需的周期非常大
而实际的置乱往往只需要十几次或者几十次,最多不超过100次就能达到很好的效果,置乱后隐藏信息再返回需要的变化次数太多,计算时间太长
0x02 改进方案描述
算法的主要流程
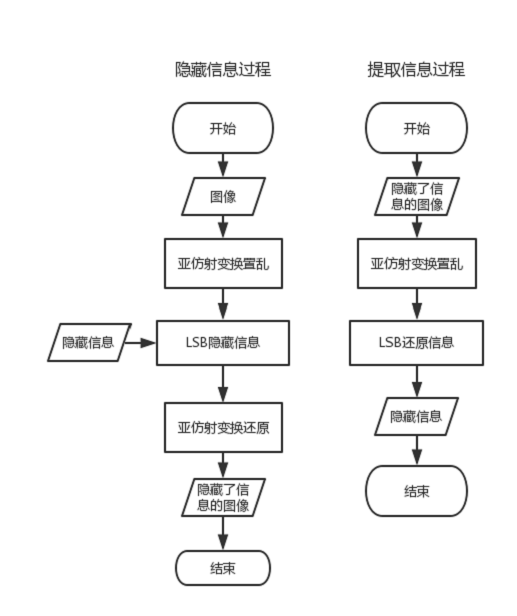
主要是改进了亚仿射变换还原过程的算法
亚放射变化和LSB的使用
我们将亚仿射变换的一种解a=0, b=-1, c=1, d=-1, e=N+1, f=1作为我们选择的参数,用这种解来进行算法实现
我们用亚仿射变化来对lena图像进行置乱
下面的图像因为传到博客的缘故不是原图,可能手机软件传输过程中压缩过
原图:512*512的RGB的Lena图像

进行1次亚仿射置乱:

进行3次亚仿射置乱:

进行5次亚仿射置乱:

进行10次亚仿射置乱:

进行20次亚仿射置乱:

进行30次亚仿射置乱:

进行50次亚仿射置乱:

进行100次亚仿射置乱:

可以看到在20次置乱时图像分布就已经非常均匀了
图像置乱之后,我们用LSB算法将信息隐藏进图像的最低有效位
还原过程的算法改进
原算法中,亚仿射变换的还原根据的是亚仿射变换的周期,图像经过一个周期的计算,才可以还原到原来的图像,图像越大周期越长,而置乱只需要较少的周期即可
亚仿射变换的周期很长,如上面现有技术方案里的原论文中的周期统计表,可以看到在尺寸为300的图像中就需要600次变换,并且尺寸越大周期越长,而置乱时无论图像大小都只需要约30~100次变换即可达到相当好的置乱效果,因此我们考虑使用一些方法,减少置乱后恢复周期的变换次数
我们注意到亚仿射变换其实是一个行列式变换,所以我们可以求出它的逆置矩阵,这样,假设尺寸300的图像经过100次置乱,原先需要再经过500次才能按周期恢复,用行列式只需要100次就可以恢复,减少400次的计算量,随着图像越大减少的计算量越多,效率越高

因此,在这个公式计算下,我们置乱图像多少次,就可以通过多少次逆计算还原原来的图像,大大减少了计算次数,较少了计算时间
0x03 效果测试
直方相交距离公式比较隐写效果

可以看到改进后的基于亚仿射变换置乱后的LSB算法计算数值相近且都接近1,并且和原方案数值相同,仍然保持了原方案抵抗直方相交距离公式分析的能力
余弦函数公式比较隐写效果
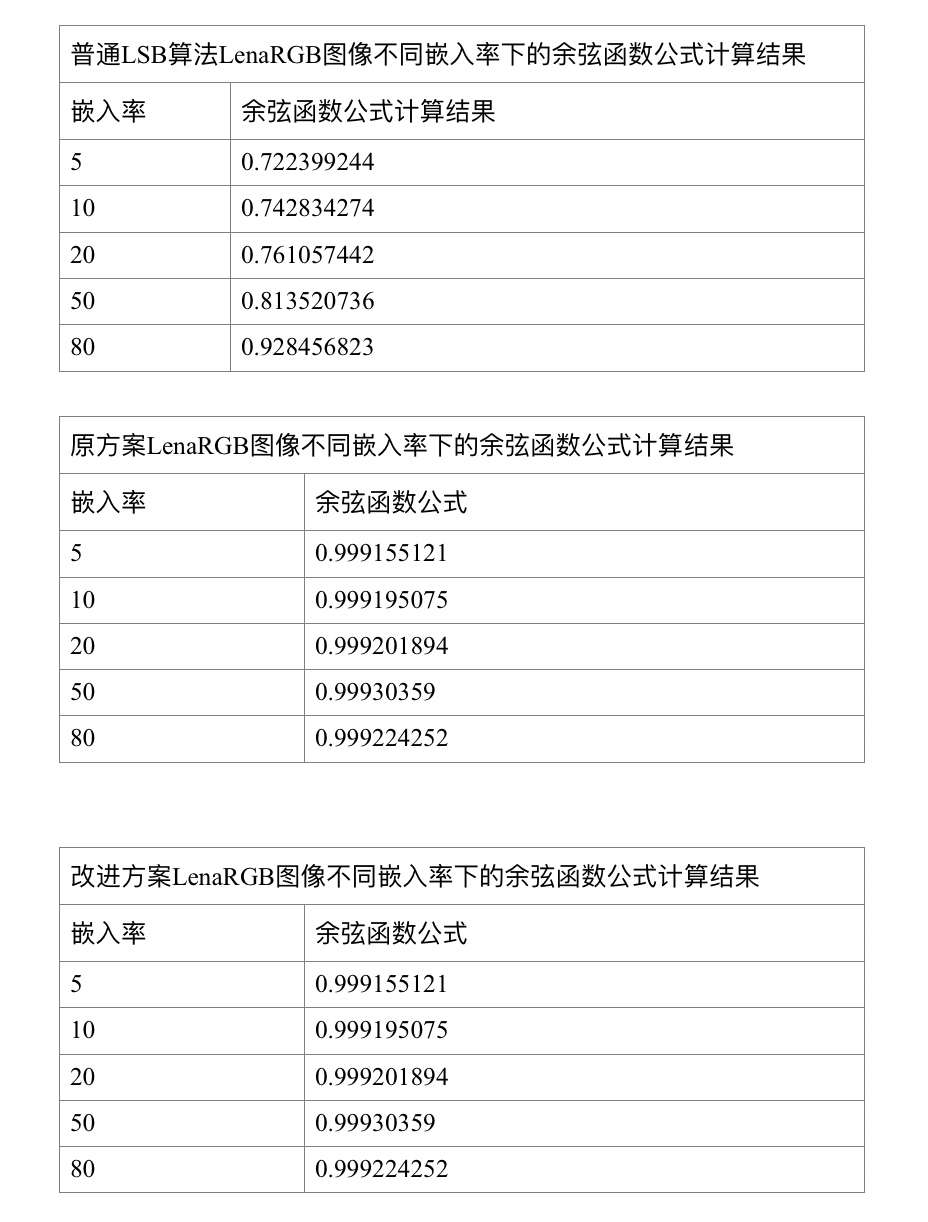
可以看到改进后基于亚仿射变换置乱后的LSB算法计算数值相近且都接近1,并且和原方案数值相同,仍然保持了原方案抵抗余弦函数公式分析的能力
RS分析法比较隐写效果
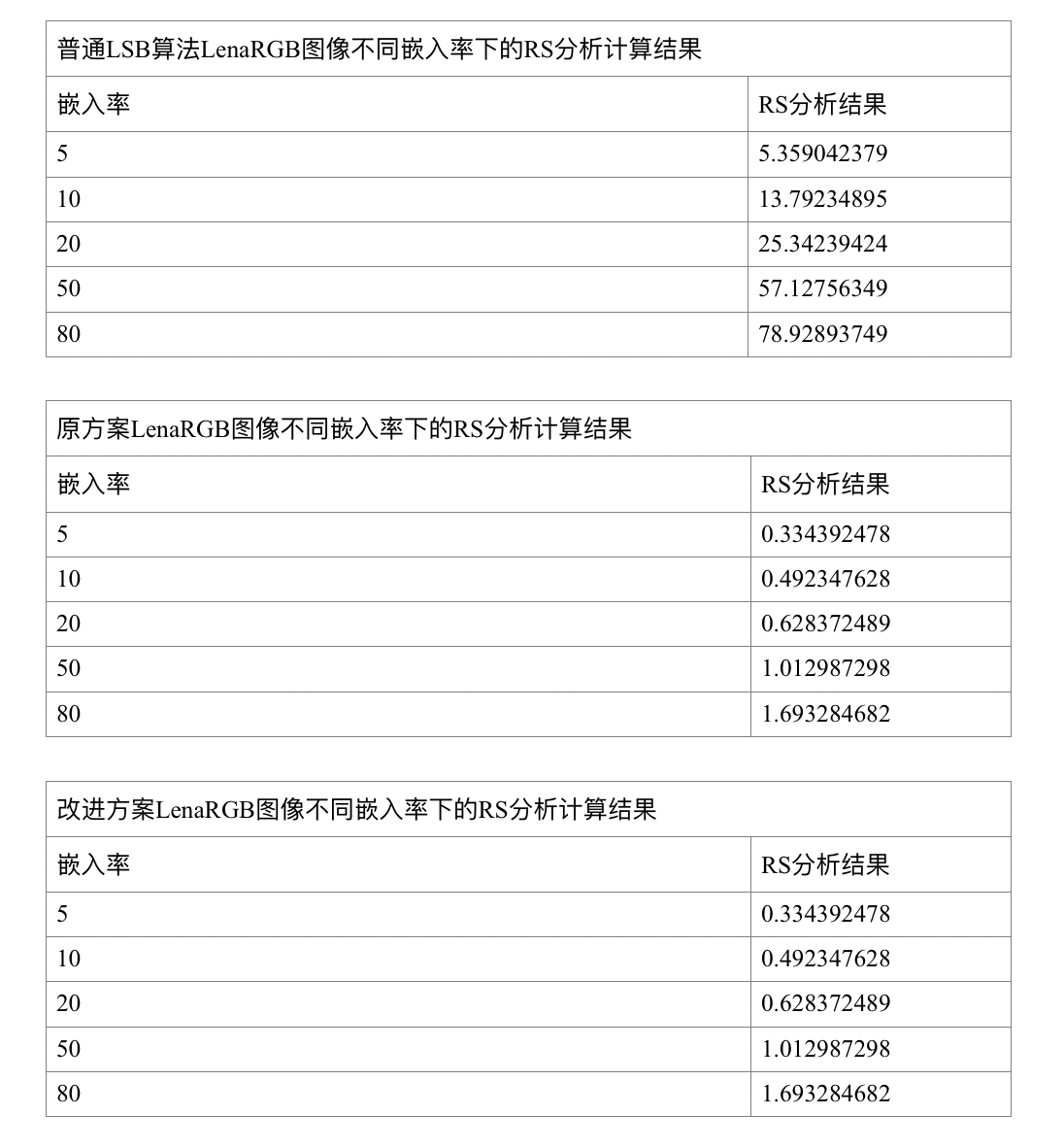
可以看到改进后基于亚仿射变换置乱后的LSB算法计算数值都比较低,并且和原方案数值相同,仍然保持了原方案抵抗RS分析法分析的能力
频度直方图比较隐写效果
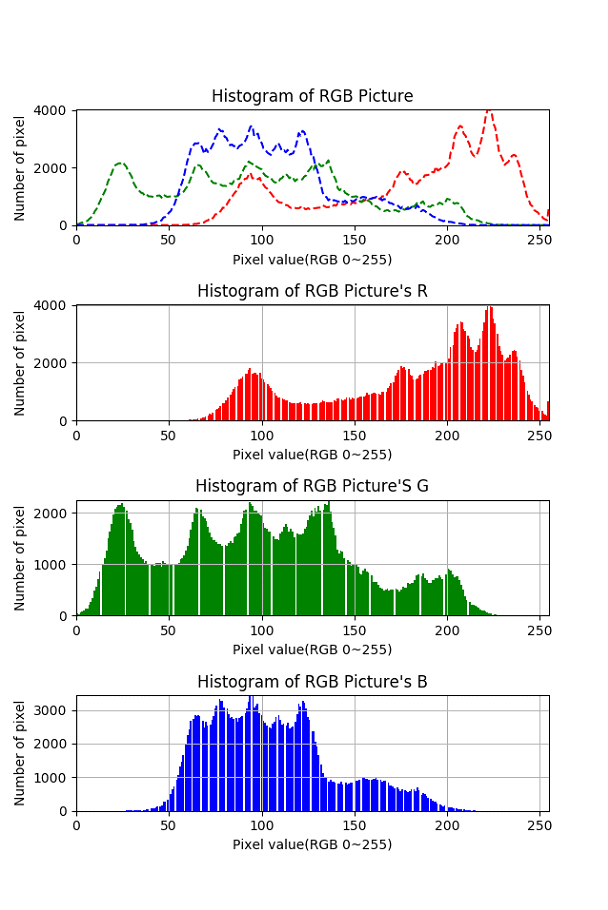
原图像频度直方图
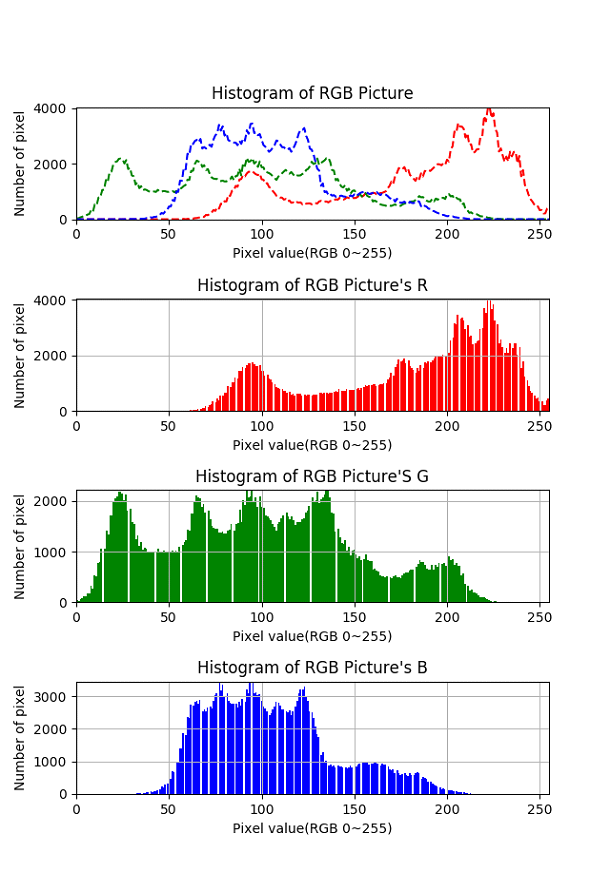
原方案隐藏信息后图像的频度直方图
改进后方案隐藏信息后图像的频度直方图
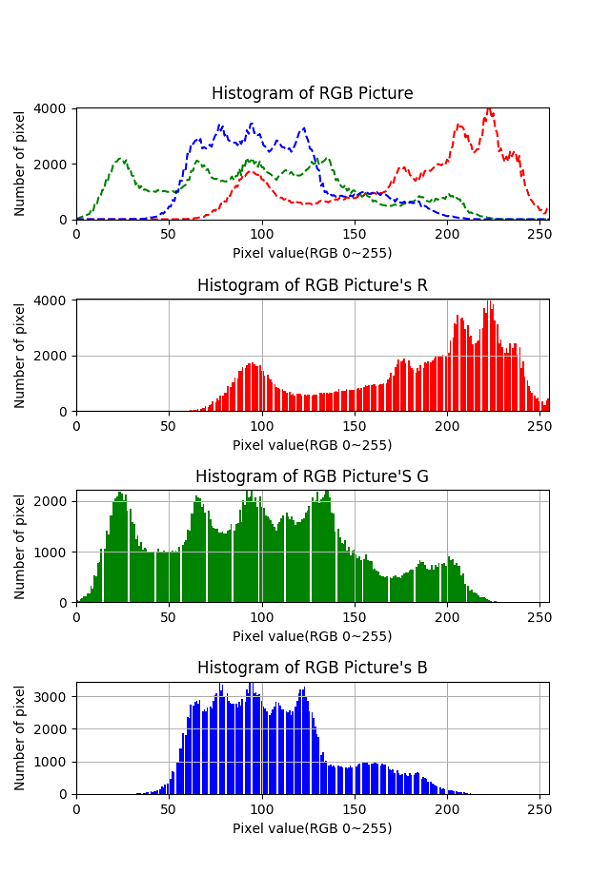
可以发现,三个对比基本看不出差别,因此可以抵抗频度直方图的分析
改进的计算速度比对
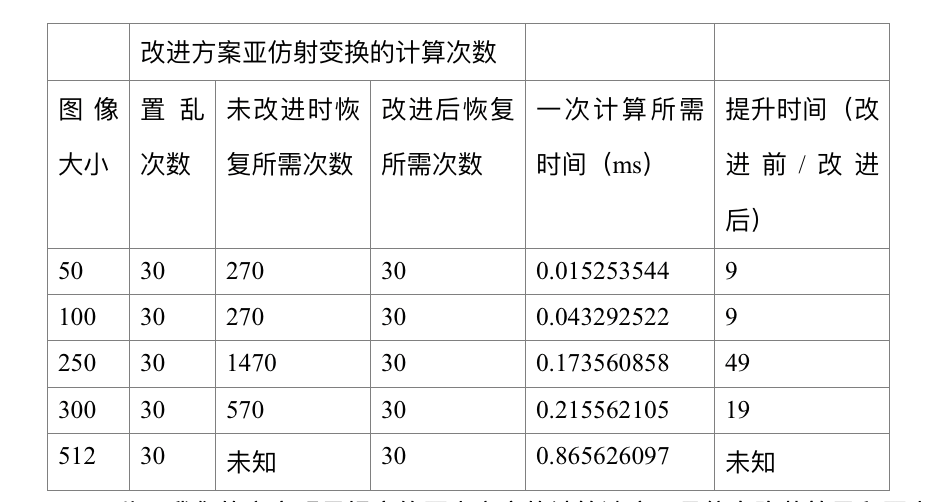
因此,我们的方案明显提高的原来方案的计算速度,且信息隐藏效果和原来方案一致(部分数据因为原方案未提供相关数据无法测试获得)
0x04 参考文档
袁占亭,张秋余,刘洪国,彭铎. 一种改进的LSB数字图像隐藏算法[J]. 计算机应用研究,2009,(01):372-374+377.

