大学里学公钥密码是RSA、Rabin、ElGamal、ECC几种,这里就写基于大数分解的RSA和基于椭圆曲线离散对数问题的ECC,其他可以关注一下
这篇写的比较粗糙,因为我相对更理解一些公钥密码,所以写做提醒自己用,有兴趣可以看我大学给老师做的公要密码加解密过程演示APP
0x00 密钥配送问题
- 事先共享密钥
- 通过密钥分配中新(KDC)解决密钥配送(依赖实现共享密钥)
- Diffile-Hellman密钥交换(和ElGamal相似)
- 公钥密码
0x01 RSA
RSA是依托于大数分解这个难题
基本加解密流程
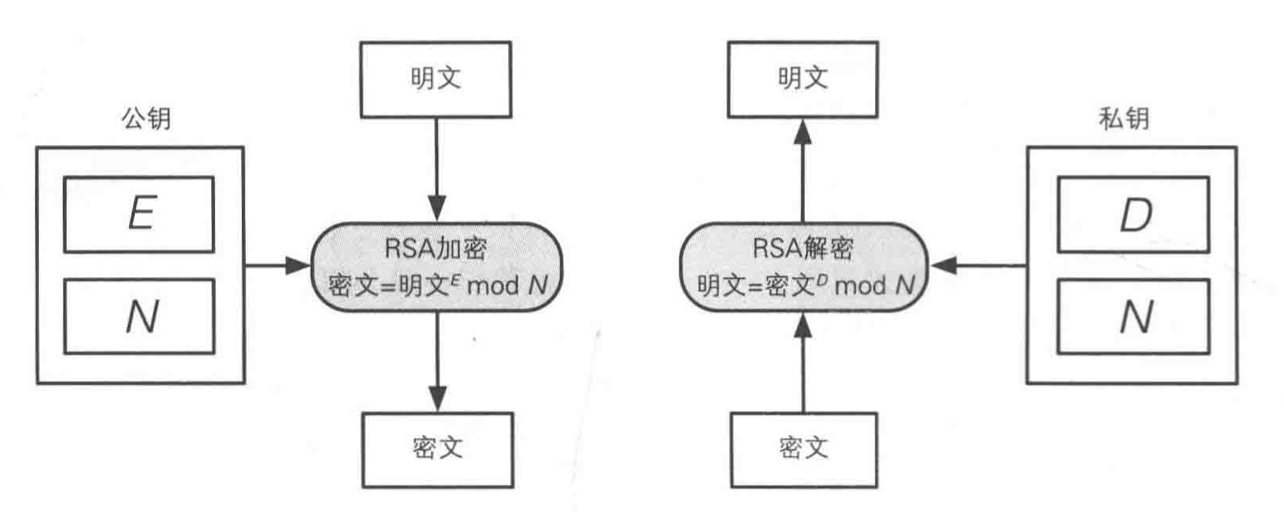
RSA密钥对的生成
大学里学的时候主要难点在于怎么用辗转相除法求公约数公倍数、米勒雷宾求素数等,以及转二进制计算次方和模运算让速度快,而不是这个流程
一图流解释密钥生成
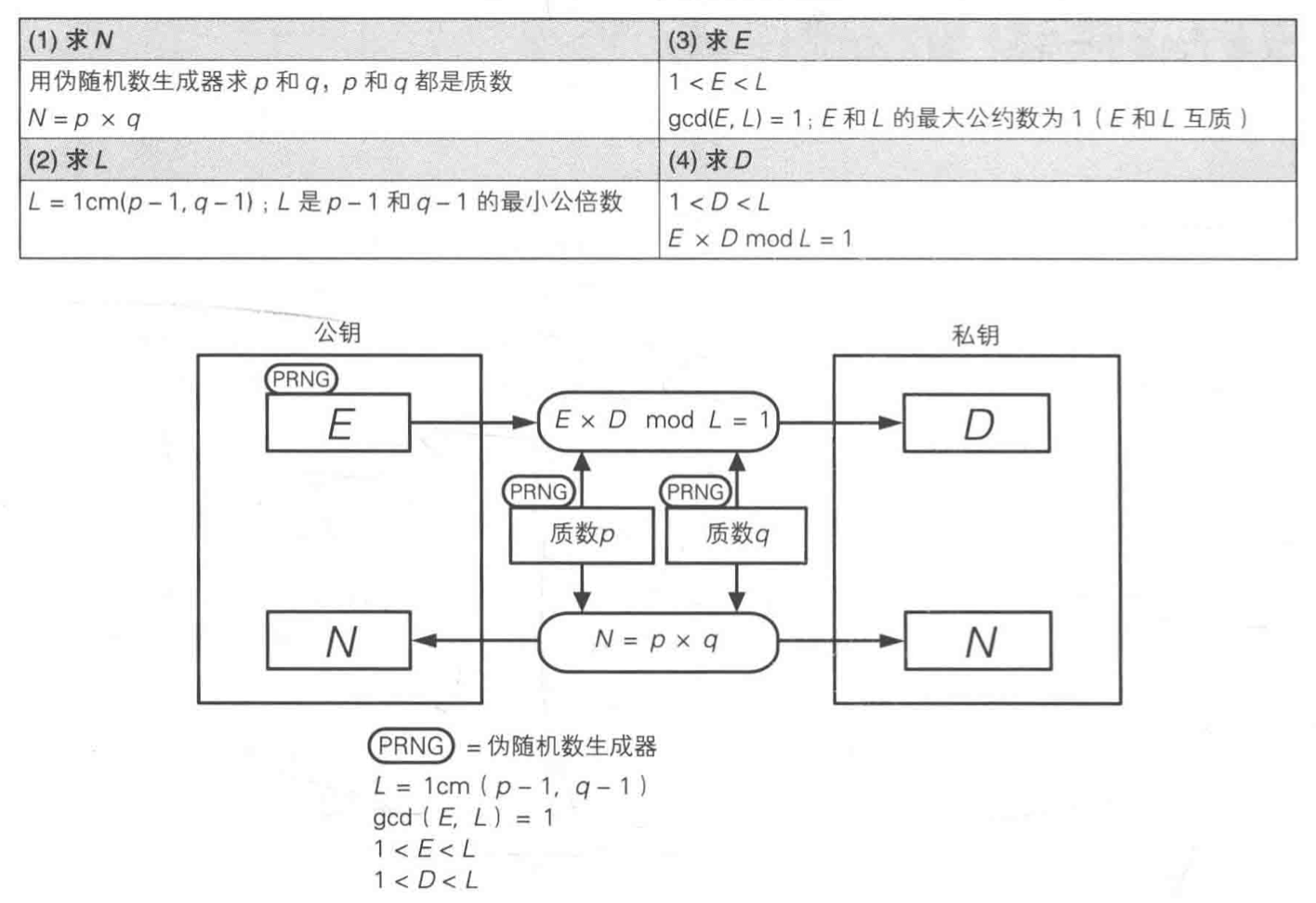
中间人攻击
一图流解释中间人攻击
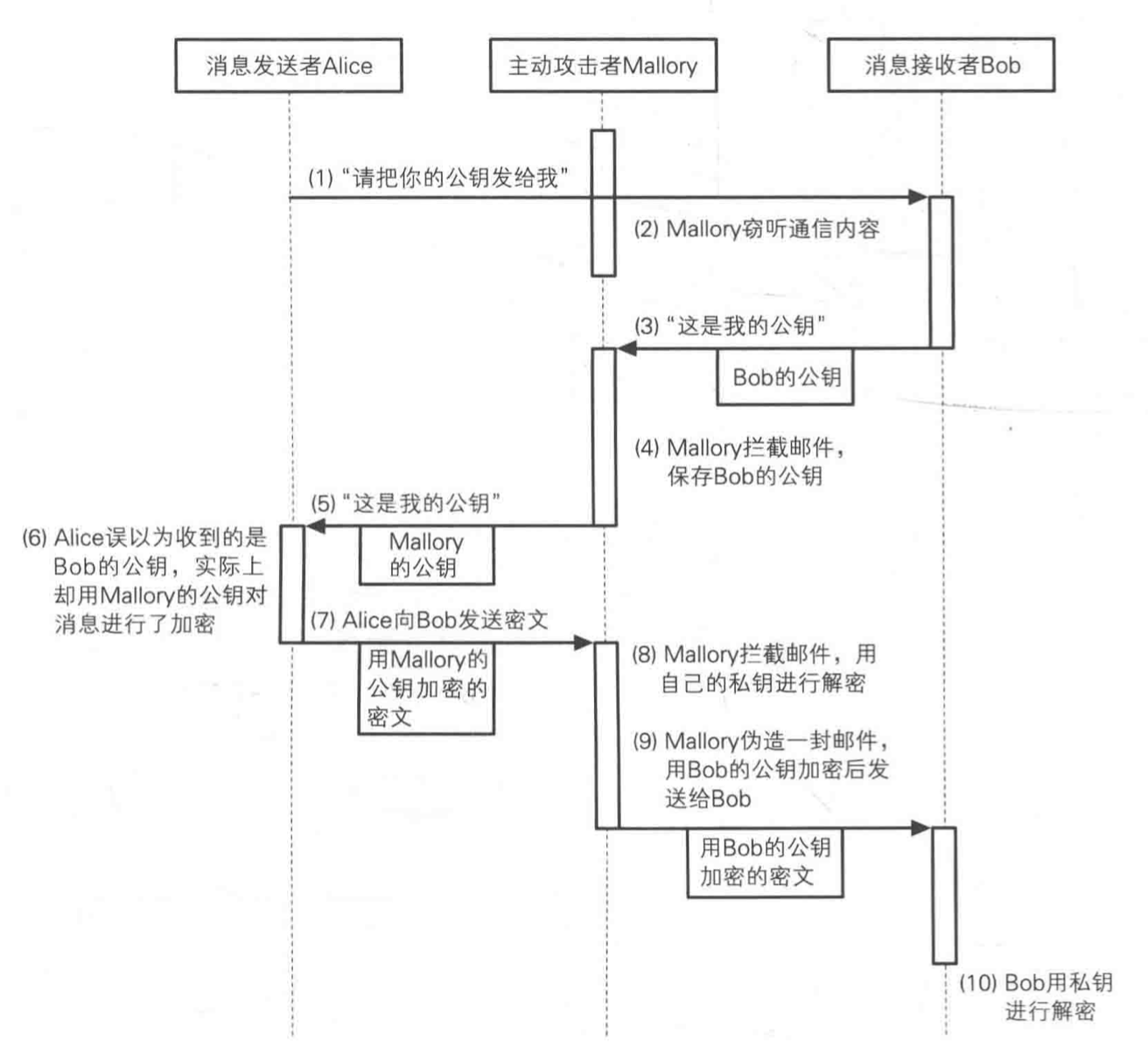
0x02 ECC
椭圆曲线密码(Elliptic Curve Cryptography)是利用椭圆曲线来实现密码技术的统称,包含
- 基于椭圆曲线的公钥密码
- 基于椭圆曲线的数字签名
- 基于椭圆曲线的密钥交换
椭圆曲线密码可以用比RSA更短的密钥来实现相同的强度
什么是椭圆曲线
公式y^2=x^3-2x+4的图像如下
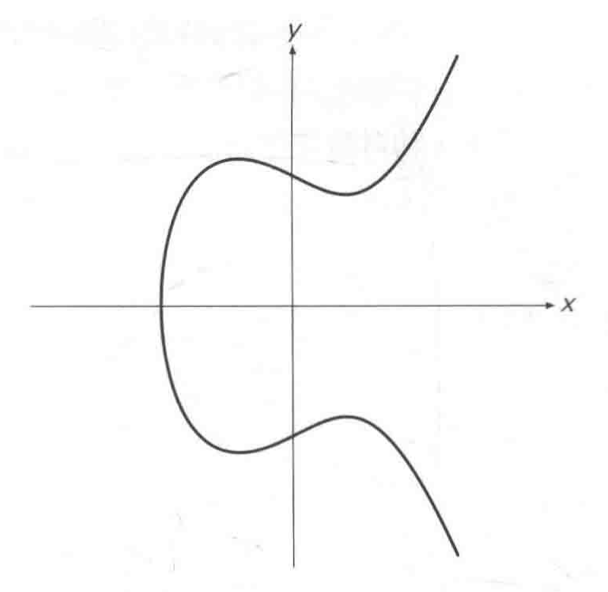
椭圆曲线离散对数问题
过曲线上两点A,B画一条直线,找到直线与椭圆曲线的交点关于x轴对称的点定义为A+B
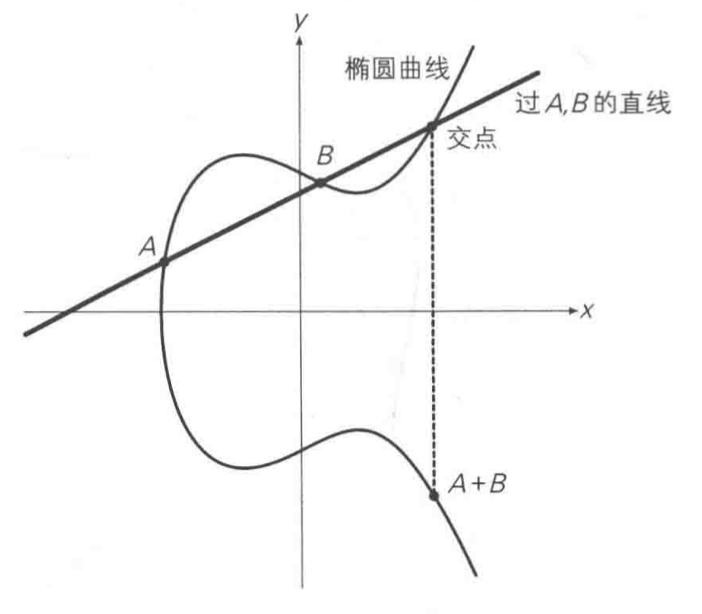
A,B为同一点时取切线,A+A如下图
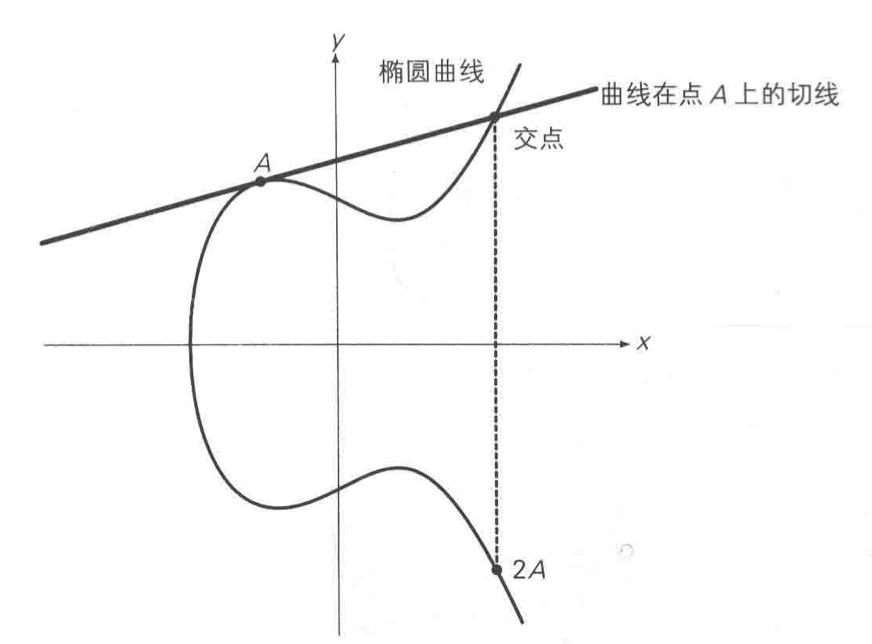
点A关于x轴对称位置的点定义为-A,如下图
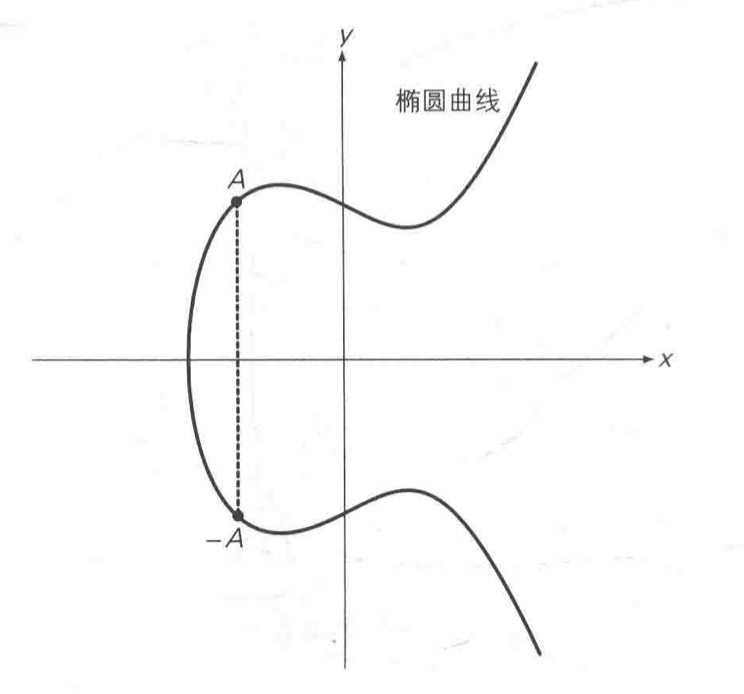
过A和-A的直线在无限远处(O)相交A+(-A)=O
按如上规则,我们给定椭圆曲线上一点G,可以求2G、3G到xG,已知数x求xG不难,但是已知xG求x很难,这就是椭圆曲线上的离散对数问题
也就是
已知
- 椭圆曲线E
- 椭圆曲线上一点G(基点)
- 椭圆曲线上一点xG(G的x倍)
求
- 数x
有限域上的椭圆曲线
上线是实数上的椭圆曲线离散对数问题,如果改成有限域上的椭圆曲线离散对数问题
也即是公示y^2=x^3+x+1(mod23),和RSA一样加上模运算
我们对上面的公式取出满足的坐标点如下
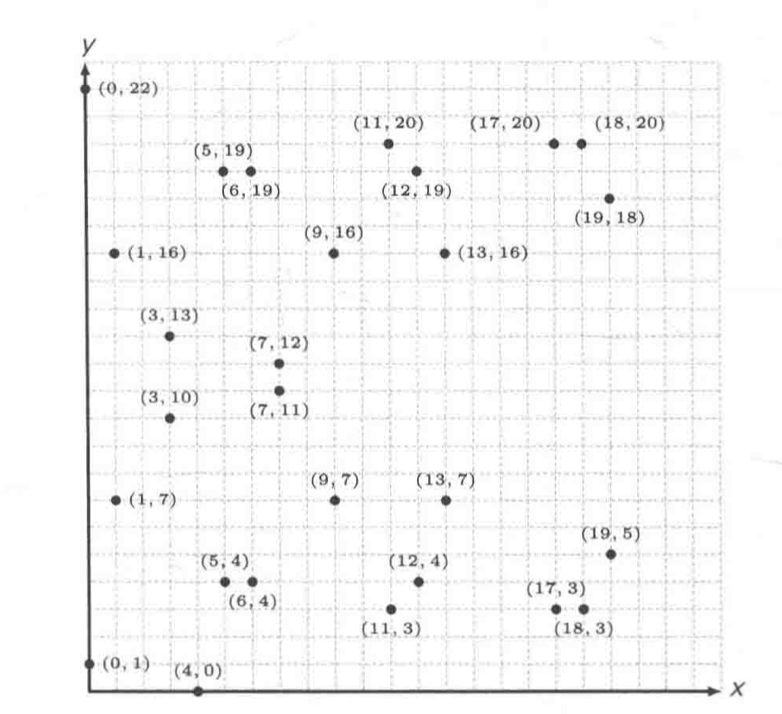
设G=(0,1),像实数集合一样求xG,点23G=(18,23),当x非常大时就很难逆推
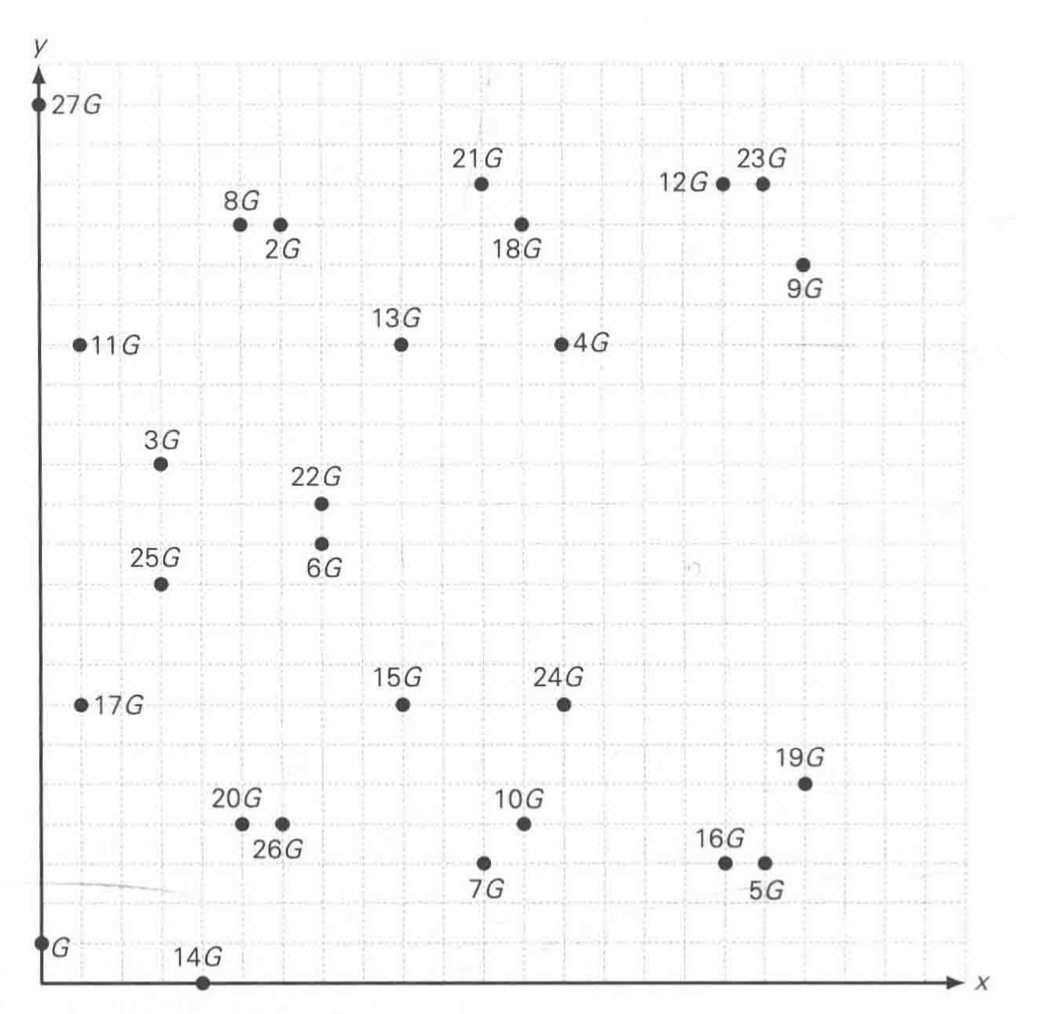
说了这么多,只要知道
- 椭圆曲线上的离散对数问题就是已知G和xG求x
- 解椭圆曲线上的离散对数问题非常困难
椭圆曲线Diffie-Hellman密钥交换
非椭圆曲线DH密钥交换利用的是以p为模,已知G和G^x mod p求x的复杂度(有限域上的离散对数问题),交换的是G^a^b中的G^a和G^b
相对的,椭圆曲线上利用已知G求xG的复杂度,交换的是abG中的aG和bG
一图流解释
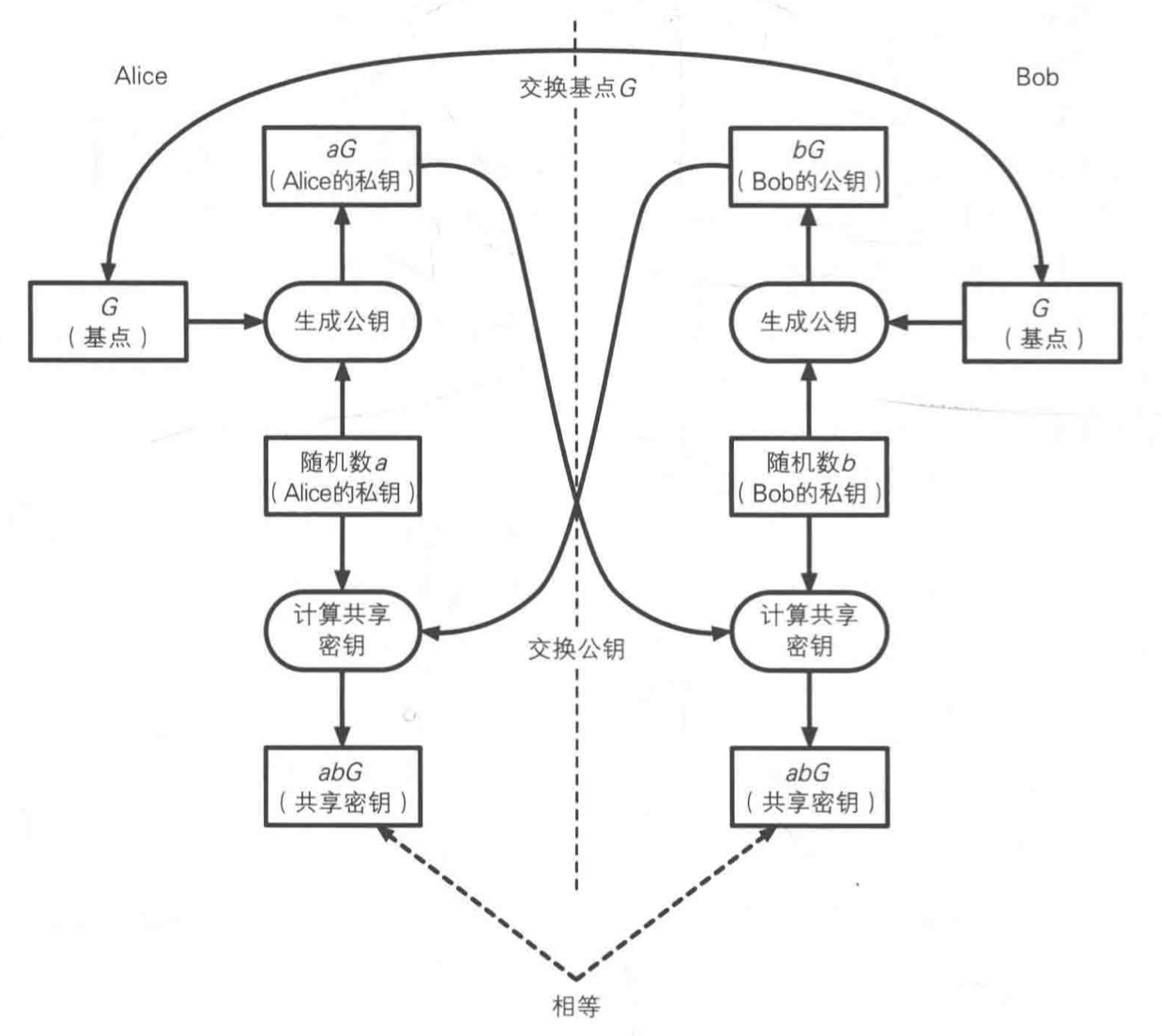
在椭圆曲线DH中,共享密钥用随机数a、b,每次通信使用不同的随机数,则共享密钥也会随之改变,由于每次通信的共享密钥不同,也无需担心之前的通信内容被破解,这种特性称为前向安全性或者完全前向安全性
椭圆曲线ElGamal密码
ElGamal密码和DH密钥交换使用的原理一样
加密
- Alice用自己的私钥a以及Bob的公钥bG,对消息M计算点
M+abG,此点M+abG就是密文 - Alice将密文
M+abG发送给Bob
解密
- Bob接受密文
M+abG - Bob用Alice的公钥aG以及自己的私钥b计算出共享密钥abG
- Bob将接受的密文
M+abG减去共享密钥abG得到消息M

