0x00 随机数的应用场景
- 生成密钥:用于对称密码和消息验证码
- 生成密钥对:用于公钥密码和数字签名
- 生成初始向量(IV):用于分组密码的CBC、CFB、OFB模式
- 生成盐:用于基于口令的密码(PBE)等
上面这些用途都很重要,但其中最重要但是生成密钥和生成密钥对两个,要做到不可预测
0x01 随机数的性质
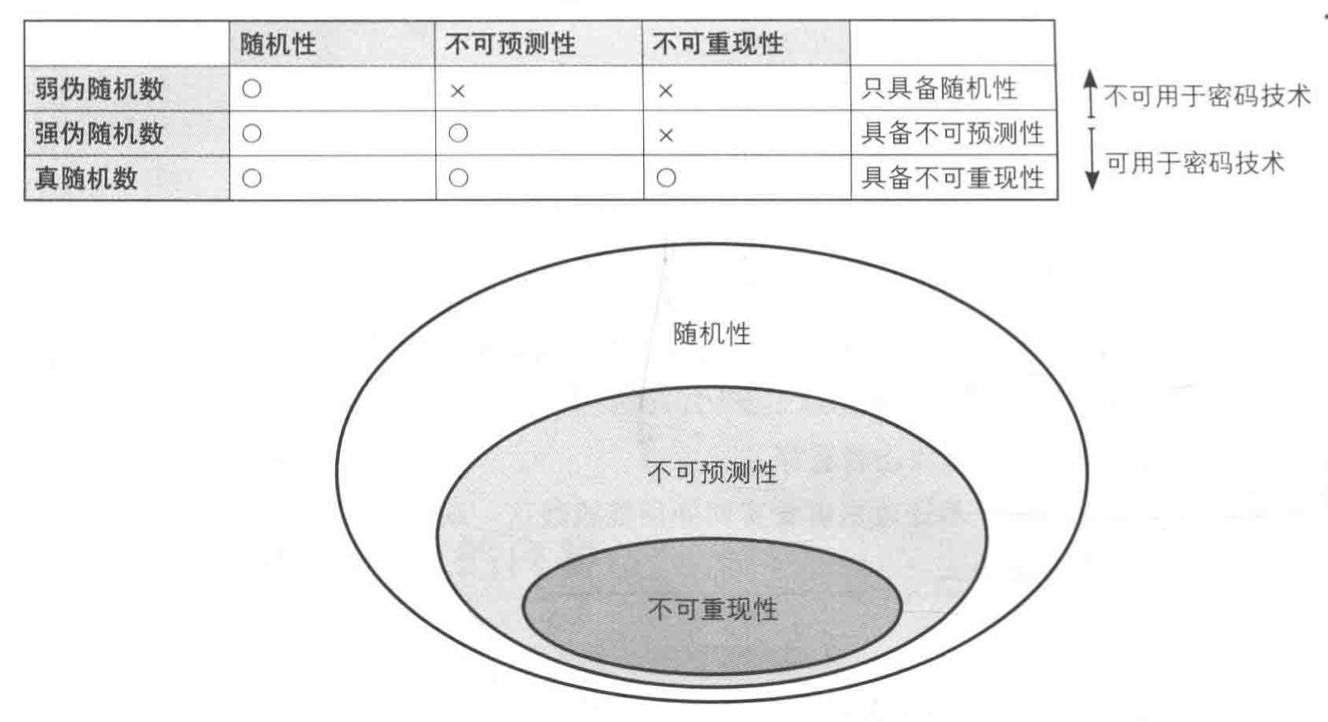
- 随机性:不存在统计学的偏差,是完全杂乱的数列
- 不可预测性:不能从过去的数列推测出下一个出现的数
- 不可重现性:除非将数列本身保存下来,否则不能重现相同的数列
0x02 伪随机数生成器
随机数可以通过硬件来生成,也可以通过软件来生成
通过硬件生成的随机数列,是根据传感器收集的热量、声音的变化等事实上无法预测和重现的自然现象信息来生成,像这样的硬件设备就称为随机数生成器(Random Number Generator, RNG)
而可以生成随机数的软件则称为伪随机数生成器(Pseudo Random Number Generator,PRNG)
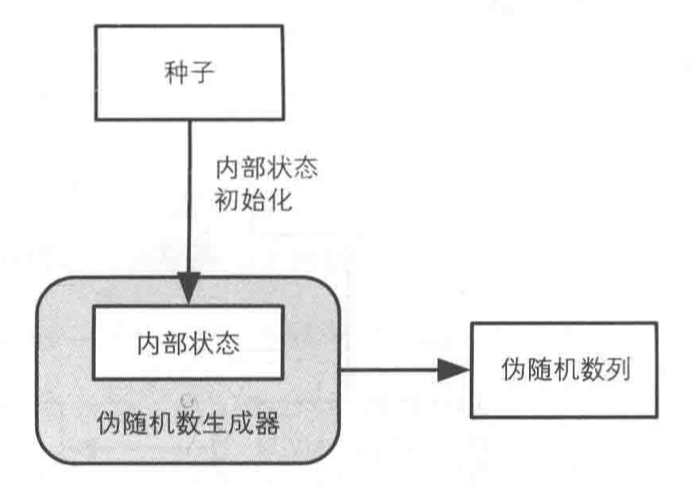
由于内部状态决定来下一个生成的伪随机数,因此内部状态不能被攻击者知道
线性同余法
线性同余法是一种使用很广泛的伪随机数生成器算法,但不能用于密码技术
假设我们要生成但伪随机数列为R0、R1、R2…Rn
R0 = (A * 种子 + C) mod M
R1 = (A * R0 + C) mod M
R2 = (A * R1 + C) mod M
...
Rn = (A * R(n-1) + C) mod M
线性同余法
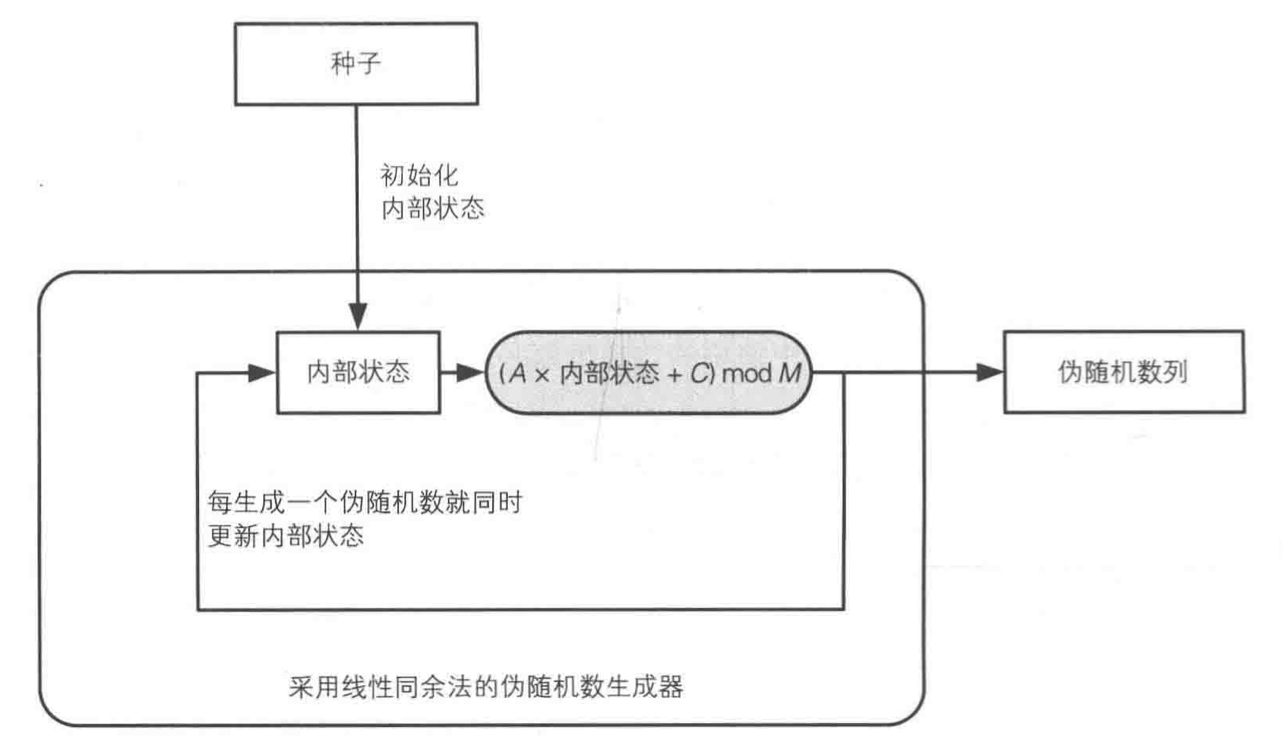
当攻击者已知Rm和ACM三个,就可以推出下一个生成的值,如果知道生成的数列,也可以反推ACM的值
线性同余法是不具备不可预测性的
单向散列函数法
这种伪随机数生成器的工作方式如下图
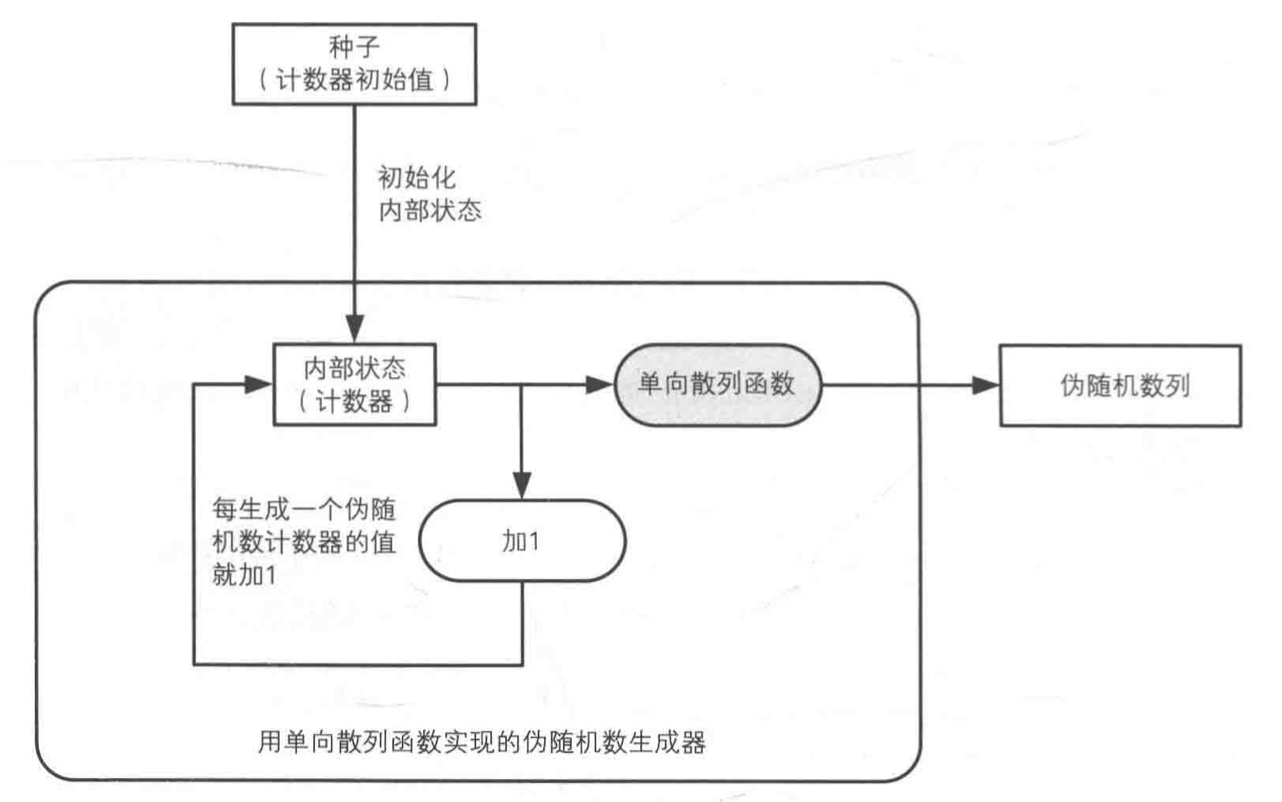
- 用伪随机数种子初始化内部状态(计数器)
- 用单向散列函数计算计算器的散列值
- 将散列值作为伪随机数输出
- 计数器加1
- 重复上面2-4步
如果攻击者要预测下一个值,需要知道计时器的当前值,这种伪随机数生成器中,单项散列函数的单向性是支持伪随机数不可预测的基础
密码法
这个方式和单向散列函数法类似
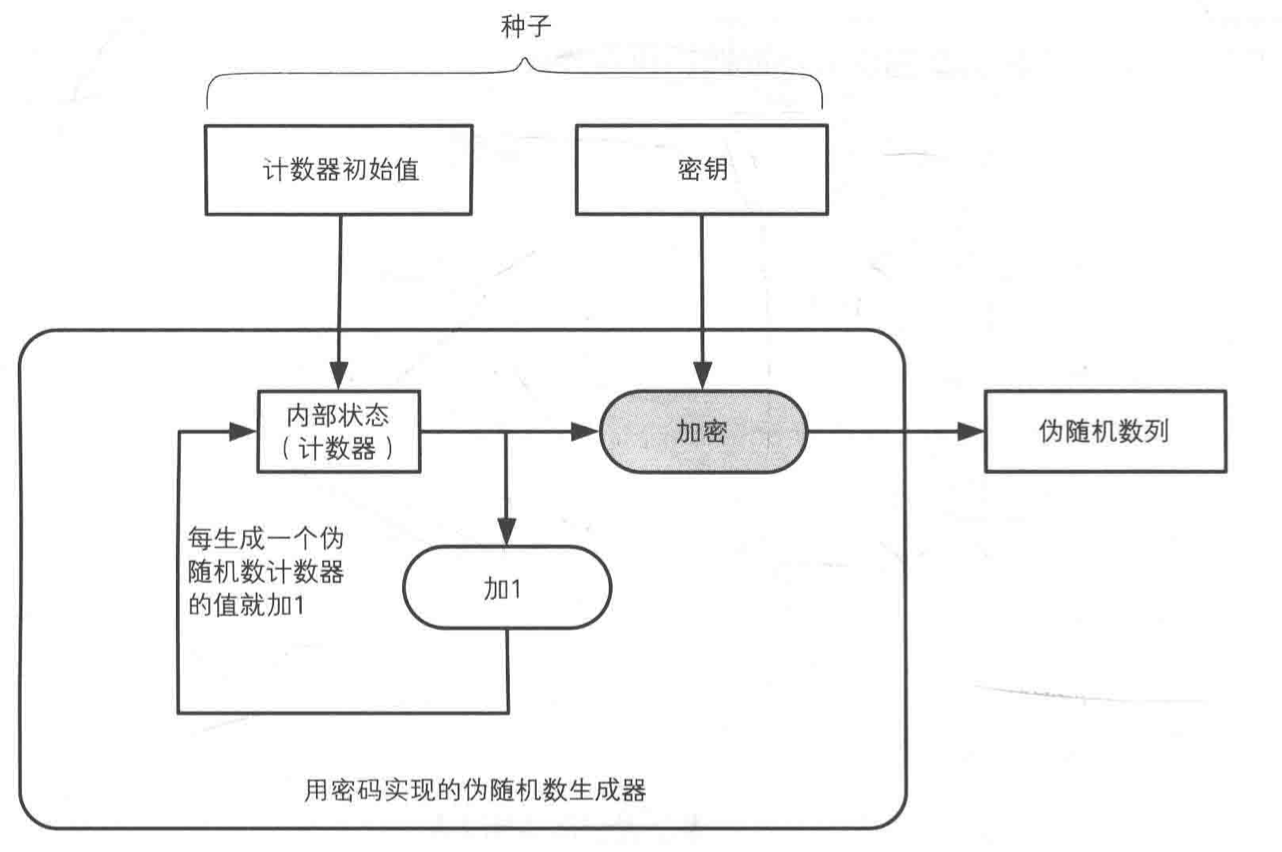
- 初始化内部状态
- 用密钥加密计数器的值(AES或者RSA等都可以)
- 将密文作为伪随机数的输出
- 计数器的值加1
- 重复上面2-4步
ANSI X9.17
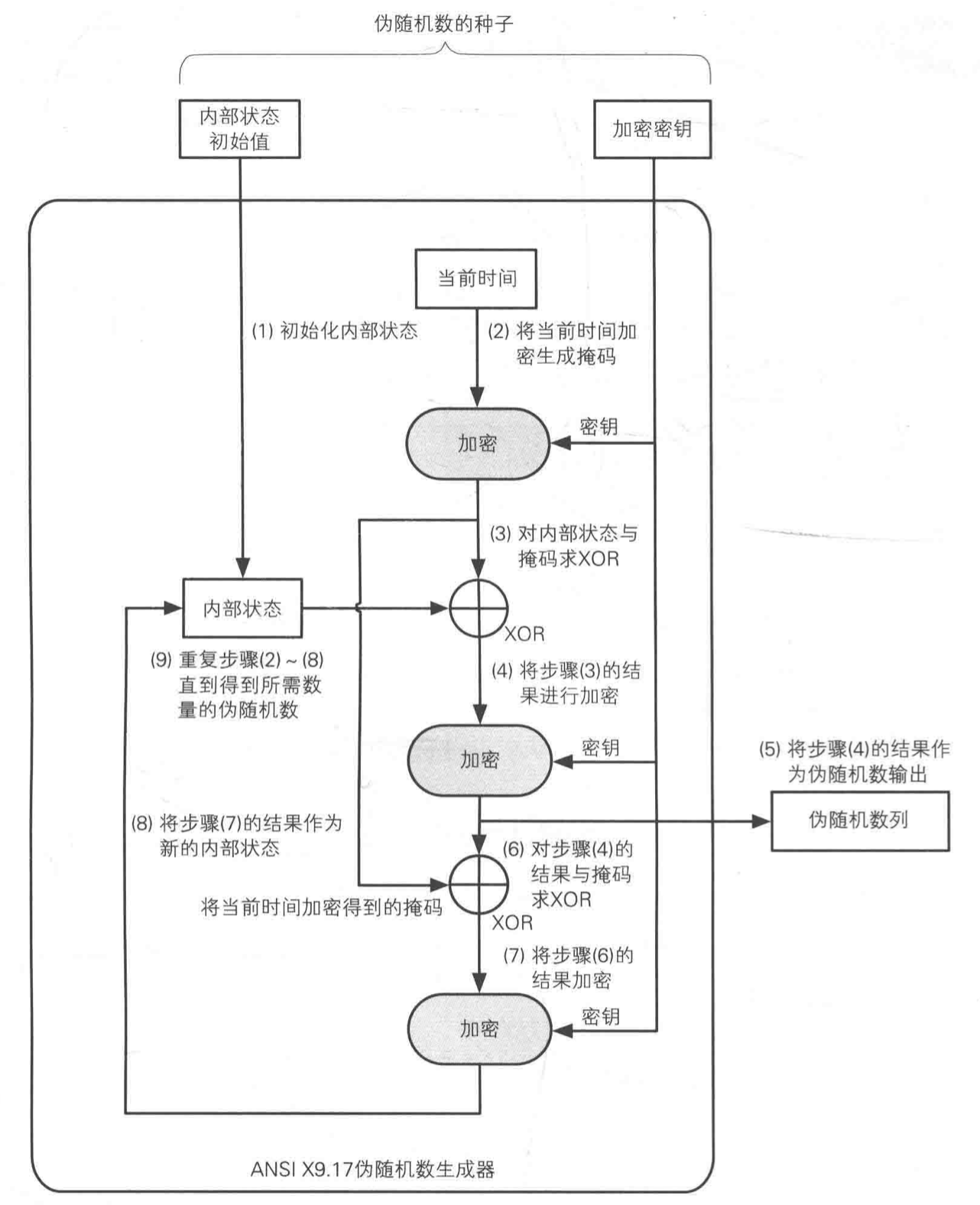
步骤2,我们将当前时间进行加密生成来一个掩码,当前时间是可以被攻击者预测的,但是攻击者不知道加密密钥,因此无法预测加密后的当前时间,在之后步骤3和6中,用掩码对比特序列进行随机翻转
步骤3-5作用是输出伪随机数,这里输出的伪随机数是将内部状态和掩码的XOR进行加密之后的结果,攻击者要看穿这个值,需要破解密码,根据过去的伪随机数数列,无法推测出伪随机数生成器的内部状态
步骤6-8的作用是更新内部状态,新的内部状态是将上一个伪随机数与掩码的XOR进行加密之后的结果,攻击者也不能从伪装随机数推测新的内部状态,因为要算出新的内部状态,还需要知道掩码以及加密密钥
0x03 伪随机数生成器的攻击
和密码相比,人们很容易忘记伪装随机数生成器也是可以受到攻击的,然而,因为伪随机数生成器承担了生成密钥的重任,因此它经常成为攻击的对象
- 对种子进行攻击:如果知道种子,就可以知道生成器生成的全部随机序列,所以种子不能泄漏
- 对随机数池进行攻击:一般不会到了需要的时候才当场生成真随机数,而是事先在一个名为随机数池的文件中积累随机比特序列,这个也不能泄漏

